E napon született 1571-ben Johannes Kepler, német bolygász és csillagász. (†1630)

1596-ban kiadott könyvében, a Mysterium Cosmographicumban (Das Weltgeheimnis) Kepler az akkor ismert hat bolygó pályáját az öt platóni testtel hozta kapcsolatba. Úgy gondolta, hogy az egyes bolygópályák gömbjei között a kocka, a tetraéder, az oktaéder, a dodekaéder és az ikozaéder tartja a távolságot.
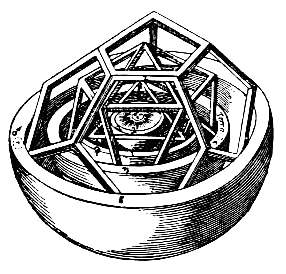
Kepler később fedezte föl a bolygómozgások törvényeit, amiket róla ma Kepler-törvényekként emlegetnek.
Kepler törvényei
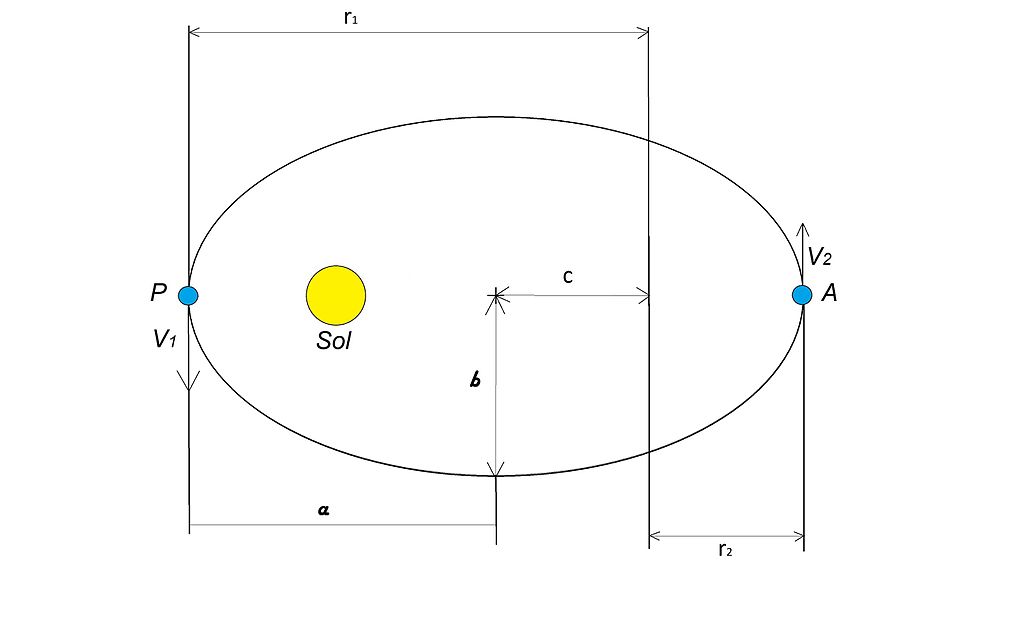
I. A bolygók pályája


ahol r és φ a bolygók napközpontú polárkoordinátái, l a fókuszon átmenő, a nagytengelyre merőleges húr fele (semi-lactus rectum), e pedig az excentricitás, azaz az elnyúltságot / lapultságot jelző arányszám.
II. A felületi törvény



III. törvény
azaz
Például a Juppiter keringési idejének (11,8 földi év) négyzete majdnem 140-szerese a Föld keringési ideje négyzetének. A Jupiter majdnem 5,2-szer van távolabb a Naptól, mint a Föld; ennek köbe szintén majdnem 140-szerese a Föld-Nap-távolság köbének.
Kepler III. törvényének pontos alakja:


ahol m a Föld – Hold rendszer össztömege, T pedig a Föld – Hold rendszer tömegközéppontjának a Nap körüli keringési ideje.
A fenti törvények általánosíthatóak: igazak egy csillag körül keringő bolygóra, egy bolygó körül keringő holdakra és műholdakra, bármely nagy tömegű égitest körül keringő más égitestekre, csupán az 

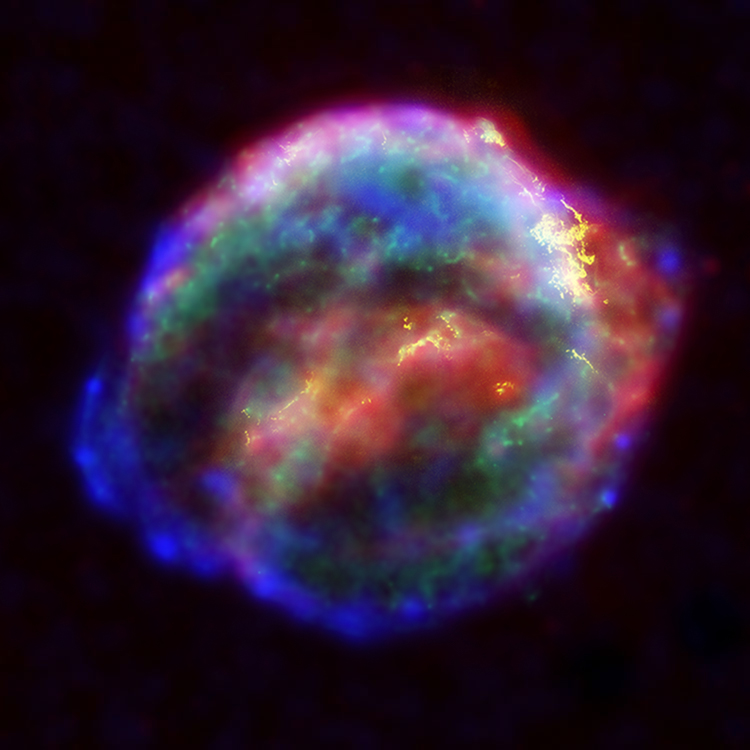
1604-ben megfigyelt egy fényes villagot (idegenkedőn szupernóvát), és bmegfigyeléseit a De Stella nova in pede Serpentarii („A Kígyótartó lábában megjelent új csillagról”) című könyvében jelentette meg.
Kepler törvényeihez hasonló vezérfonalat kell adni ma az ifjúságnak, hogy Mammón meg a nigráns-áradat el ne nyelje magyar fiainkat mind egy szálig…
Beteg világunkban érdemes lenne végre rendet tenni !!! Legalább a Magyar Világban !!!
Ifjaink fölösleges kütyüzsibbadásai helyett pedig egy bölcsebb világban kezdhetnék végre Madách Imre Kepler-színét (a Nyolcadik színt) zsolozsmázni minden leendő férfi tanulságára…
Kétséges rang-e hát szellem, tudás?
Homályos származás-e a sugár,
Amely az égből homlokomra szállt?
Hol van nemesség más ezen kivűl?
Amit ti úgy neveztek, porlatag,
Hanyatló báb, mit lelke elhagyott,
De az enyém örök-ifjú, erős.
– Oh nő, ha te meg bírnál érteni,
Ha volna lelked oly rokon velem,
Minőnek első csókodnál hivém,
Te büszke lennél bennem, s nem keresnéd
Kivűl a boldogságot körömön,
Nem hordanál mindent, mi benned édes,
Világ elé s mindent, mi keserű,
Nem tartanál fel házi tűzhelyednek. –
Madách Imre: Az ember tragédiája
Ez intelem pedig leányainknak is illő okulására válik !

Aki pedig ennél is behatóbb tudásra, az eredetire vágyik, annak álljanak itt…
Kepler fönnmaradt művei
- Mysterium cosmographicum (A kozmosz szent titka) (1596)
- Astronomiae Pars Optica (A csillagászat optikai része) (1604)
- De Stella nova in pede Serpentarii (Új csillag a Kígyótartó lábánál) (1604)
- Astronomia nova (Új csillagászat) (1609)
- Tertius Interveniens (1610)
- Dissertatio cum Nuncio Sidereo (Beszélgetések a csillaghírnökkel) (1610)
- Dioptrice (Dioptria) (1611)
- De nive sexangula (A hatszögletű hópehelyről) (1611)
- De vero Anno, quo aeternus Dei Filius humanam naturam in Utero benedictae Virginis Mariae assumpsit (A valódi évről, amelyben az örök Isten Fia az áldott Szűz Mária méhében emberként megfogant) (1613)
- Eclogae Chronicae (Krónika fejezetek) (1615)
- Nova stereometria doliorum vinariorum (A boroshordók új térfogatméréséről) (1615)
- Epitome astronomiae Copernicanae (Kivonat a kopernikuszi csillagászatról) (három részben 1618–1621 között)
- Harmonice Mundi (Világok harmóniája) (1619)
- Mysterium cosmographicum (A kozmosz szent titkai) Második kiadása (1621)
- Tabulae Rudolphinae (Rudolf-táblázatok) (1627)
- Somnium, sive Opus posthumum de astronomia sublunari (Az álom – Posthumus mű a holdbéli csillagászatról) (1634)
Ha tetszik írásunk, ajánlhatja másoknak is!
A túlélés útja ma magyarul gondolkodni...












 Európa szívéből
Európa szívéből





.jpg)






















